Compiler-As-3

Question 1

Use the grammar rules and attribute definitions in Lecture 10 Page 19 to construct the parse tree and syntax tree for expression " $(3 + 1) - (4 - b)$ " assuming the expression is tokenized as " $(n u m + n u m) - (n u m - i d)$ " $(20 p t)$

Parse Tree:

Tree

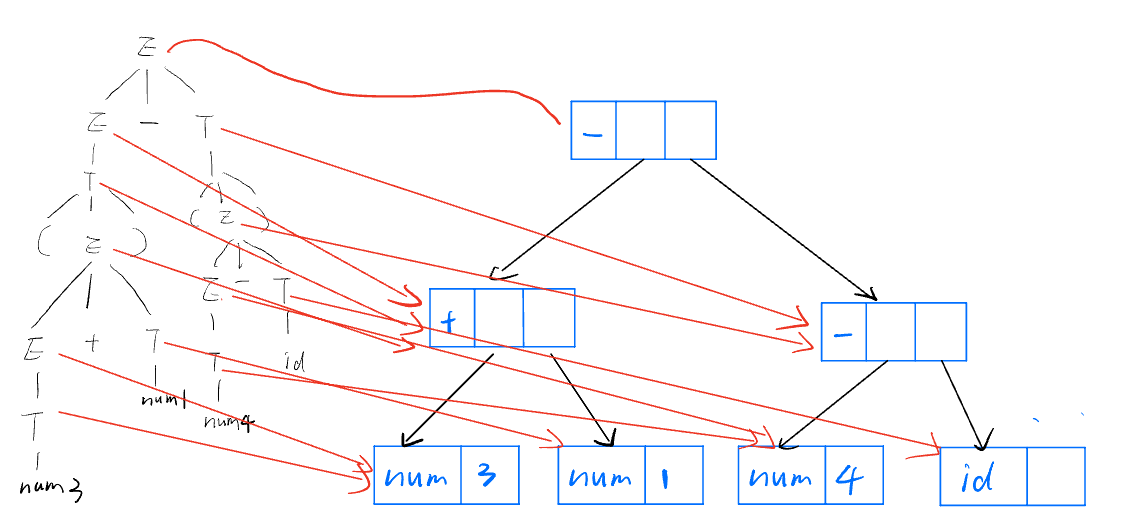
Syntax Tree: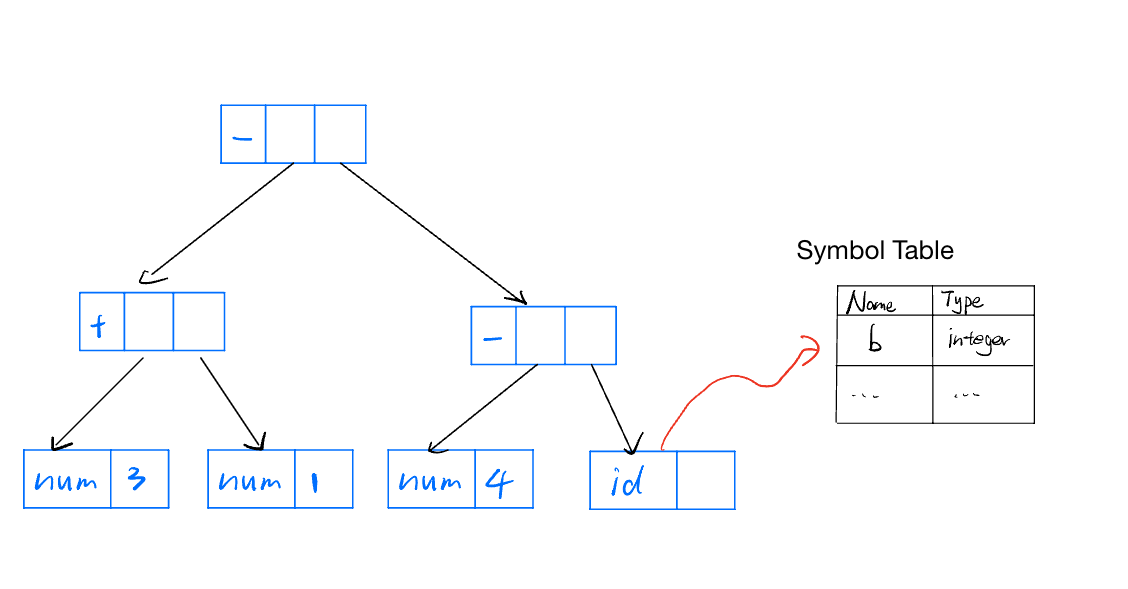

Question 2

Use the grammar rules and attribute definitions in “Grammar+Typing.docx” (the grammar is in Lec 12 on pg 20) to analyze the source code

python

bool flip(bool x) not x; flip (flase)

Parse Tree

Symbol Table

Name	Type
flip	$b o o l \to b o o l$
~~x （Removed）~~	$b o o l$

Question 3

The language in Lec 11 on Page 27 has two production rules:

1. T_{1} \to T_{2} *

2. T_{1} \to T_{2} [n u m]

So, it is possible to have valid variable declarations

int *[10]x; int[10]* y;

Please follow the corresponding type checking rules on the same page to give the type of $x$ and $y$ . You need to explain your answer. $(15 p t)$

The type of x is $a r r a y (0 \dots 9, p o i n t e r (i n t . t y p e))$ The type of y is $p o i n t e r (a r r a y (0, 9, i n t . t y p e))$

Question 4

The language in Lec 11 on Page 27 is too weak. It cannot make assignment from a memory location to a pointer. Thus, we power-up the language by modifying the grammar rules. (New or modified rules are in red color.) Define the correct type checking rules for the new grammar rules. Type checking for old grammar rules remain unchanged. $20 p t$

$P \to D;$ $S;$ $E$
$D_{1} \to D_{2}; D_{3}$
$D \to T i d$
$S_{1} \to S_{2}; S_{3}$
$S \to I = R$
$I \to i d$
$I \to i d [E]$
$R \to & i d$
$R \to E$
$T_{1} \to c h a r$
$T_{1} \to i n t$
$T_{1} \to T_{2} *$
$T_{1} \to T_{2} [n u m]$
$E \to c h a r_l i t$
$E \to n u m$
$E \to i d$
$E_{1} \to E_{2} m o d E_{3}$
$E_{1} \to * E_{2}$
$E_{1} \to E_{2} [E_{3}]$

$R \to E$ $R . t y p e := E . t y p e$

$R \to & i d$
$i f (i d . i s_v a r i a b l e == t r u e)$

t h e n R . t y p e := p o i n t e r (l o o k_u p (i d . e n t r y)))

e l s e R . t y p e := t y p e_e r r o r

$I \to i d [E]$
$i f (E . t y p e == i n t . t y p e a n d l o o k_u p (i d . e n t r y) == a r r a y (i, t) a n d E . v a l < i a n d E . v a l >= 0)$

t h e n I . t y p e := t

e l s e I . t y p e := t y p e_e r r o r

$I \to i d$ $I . t y p e := l o o k_u p (i d . e n t r y)$

$S_{1} \to S_{2}; S_{3}$ no need to define type $S \to I = R$ no need to define type $P \to D;$ $S;$ $E$ no need to define type

Question 5

Let the following grammar rules be the syntax of integer arithmetic.

$E \to E + T$
$E \to T$
$T \to T \times F$
$T \to F$
$F \to (E)$
$F \to n u m$

Remark:

Token "num" is an integer constant.
"+" and "×" are integer addition and multiplication respectively. Multiplication has the higher precedence. Furthermore, both operators are (left and right) associative.

However, this language is not perfect. It may contain many redundant parentheses.

For example, ((2 × 3) + 4) can be entirely without the parentheses as 2 × 3 + 4. (You can try to parse them.) Thus, please design semantics for the grammar rules to remove redundant parentheses. (25 pt)

Hint:

The semantics should have at least two attributes.
One attribute is "expression", which holds the expression for each substructure.
After computing the semantics, E.expression has the final outcome — the arithmetic expression without useless parentheses.
The value of attribute "expression" is treated as a string. And the operator " $\circ$ " can be used (in semantic rules) to concatenate two strings.

Define the semantics for the grammar rules.

expression: Stores the simplified expression without redundant parentheses.
priority: Stores the priority of the operator in the expression.

$\circ$ denotes the concatenation of two strings.

Define a function for checking whether parentheses are needed for a given expression.

python

function checkParen(childExpr, childPriority, parentPriority):
    if childPriority < parentPriority then
        return "(" + childExpr + ")"
    else
        return childExpr

$E \to E_{1} + T$
- $E . p r i o r i t y = 1$
- $E . e x p r e s s i o n = E_{1} . e x p r e s s i o n \circ + \circ T . e x p r e s s i o n$
$E \to T$
- $E . p r i o r i t y = T . p r i o r i t y$
- $E . e x p r e s s i o n = T . e x p r e s s i o n$
$T \to T_{1} \times F$
- $T . p r i o r i t y = 2$
- $T . e x p r e s s i o n = c h e c k P a r e n (T_{1} . e x p r e s s i o n, T_{1} . p r i o r i t y, T . p r i o r i t y) \circ \times \circ c h e c k P a r e n (F . e x p r e s s i o n, F . p r i o r i t y, T . p r i o r i t y)$
$T \to F$
- $T . p r i o r i t y = F . p r i o r i t y$
- $T . e x p r e s s i o n = F . e x p r e s s i o n$
$F \to (E)$
- $F . p r i o r i t y = E . p r i o r i t y$
- $F . e x p r e s s i o n = E . e x p r e s s i o n$
$F \to num$
- $F . p r i o r i t y = 3$
- $F . e x p r e s s i o n = n u m$

Algorithm

Tutorial

assignment

Assignment

As-1

As-2

Lab-1

Lab-2

Lab-3

Lab-4

GAMES101

Assignment-1

Assignment-2

Assignment-3

Assignment-4

Lab

Lecture

Peoject

CSCN

Ploidy

Compiler-As-3 ​

Question 1 ​

Question 2 ​

Question 3 ​